简注 - A Tutorial on White-box AES

白盒密码是对非可信平台下的密码算法安全实现的研究。其针对密码学算法在非可信平台设计实现，使得软件（数字内容）在具有完全操控（debugger，assembler）情况下获得安全保护。论文[^1]简要介绍AES在白盒攻击环境 (White-box Attack Context) 下AES的一种实现方式及其密码学分析。

简介

白盒密码学 (White-box Cryptography) 意图设计特定实现，使得软件、数字资源等在不安全（非受信任）的环境下保护软件、资源的安全。白盒密码设计分析不同于像代码混淆[^2][^3]、控制流混淆这样的反逆向工程机制，它是纯粹针对算法安全性进行设计与分析[^4]。几乎所有的白盒密码学设计都针对对称加密算法，AES的设计就是典型之一。最初的白盒AES、DES由S. Chow，et.al 实现[^5]，后来该算法被攻破。随后不同的学者也相继发明了各种WBAC下的实现。
根据Alex, et.al 对白盒的时间进行了分类：强白盒设计与弱白盒设计[^7]。弱白盒设计要求算法实现能保护密钥不可被发现与推导，保护密钥不受密钥恢复攻击(key recovery attack)。这种实现对于查表的逆向推导理论上是不可防护的。强白盒设计要求解密器不可从加密器推导，i.e.,_plaintext-recovery attack_。chow的实现是白盒的开篇，应该归类为弱白盒实现。

AES与矩阵查表操作

AES拥有4个变换：轮钥加 (AddRoundKey)、行变换 (ShiftRows)、列混淆 (MixColumns)、字节替换 (SubBytes)[^6]。这些操作都可以归结为查表操作。查表操作的可逆转性是非常强的，很容易得到原生结果。
其中，行变换是线性的，跟轮钥加可以进行位置上的替换。只要先对原有矩阵进行行变换，然后异或行变换过的轮密钥，这样这两个操作跟原有设计结果上没有差别。其次我们可以把第一轮异或加入到循环中，最后一轮异或移出循环。这种数学上的正确性有利于我们对AES查表操作 (table lookup) 性质的解析。
得到的结果：

state <- plaintext
for r = 1 to 9:
	ShiftRows(state)
	AddRoundKey(state, k1[r-1])
	SubBytes(state)
	MixColumns(state)
ShiftRows(state)
AddRoundKey(state, k1[9])
SubBytes(state)
AddRoundKey(state, k1[10])
ciphertext <- state

其中，k1[r-1]是进行行变换过的轮密钥。

上述算法描述中，AddRoundKey 和 SubBytes 可以对原有的S-Box合并：

T-boxes

$$
T^r_i(x) = S(x \oplus k1_{r-1}[i]), (i = 0…15, r=1…9)
$$

$$
T^{10}i(x) = S(x \oplus k1_9[i]) \oplus k1{10}[i], (i = 0…15)
$$

这又叫AddRoundKey SubBytes构成的 $T-boxes$，其中x代表一个4x4矩阵中的一个字节，i代表第0～15个字节，r是轮次，S是S-Box的查表操作。每轮16个表，一共160表。（矩阵变换）。

MixColumns推导成：

$T_{y_{i}}$ 表

列混淆是纯粹查表变换。将混淆矩阵作用于4x4状态的每一列。
MixColumns表：
$$
MC = \begin{bmatrix} 02 & 03 & 01 & 01 \\ 01 & 02 & 03 & 01 \\ 01 & 01 & 02 & 03 \\ 03 & 01 & 01 & 02 \end{bmatrix}
$$
列混淆操作为混淆矩阵MC左乘状态矩阵中的每一列，对其进行行变换：
$$
\begin{bmatrix} 02 & 03 & 01 & 01 \\ 01 & 02 & 03 & 01 \\ 01 & 01 & 02 & 03 \\ 03 & 01 & 01 & 02 \end{bmatrix} \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{bmatrix}
$$
其中$x_i$是一列中的一个字节。

这等同于MC中每一列在x$下$的线性组合:
$$
MC \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{bmatrix} = x_0 \begin{bmatrix} 02 \\ 01 \\ 01 \\ 03 \end{bmatrix} \oplus x_1 \begin{bmatrix} 03 \\ 02 \\ 01 \\ 01 \end{bmatrix} \oplus x_2 \begin{bmatrix} 01 \\ 02 \\ 02 \\ 01 \end{bmatrix} \oplus x_3 \begin{bmatrix} 01 \\ 01 \\ 03 \\ 02 \end{bmatrix}
$$

将每个字节的求积拆解，即为如下变换相异或：
$$
T_{y_0} (x) = x \cdot \begin{bmatrix} 02 & 01 & 01 & 03 \end{bmatrix} ^T \\
T_{y_1}(x) = x \cdot \begin{bmatrix} 03 & 02 & 01 & 01 \end{bmatrix} ^T
$$

此处的entry x，对应着$x_0, x_1, x_2…$。
剩下的好推。

最后结果应该为：
$$
T_{y_0}(x_0) \oplus T_{y_1}(x_1) \oplus T_{y_2}(x_2) \oplus T_{y_3}(x_3)
$$

这里，

XOR 表

也是需要的。
$$
XOR(x, y) = x \oplus y
$$
这里采用4比特表，即x、y为4比特。（为什么要这么做还不太清楚，也许8比特表太大？）则每一列需要32/4 = 8个XOR表，把$T_{y_i}$表变换来的4个32位字异或成32位的最终结果。

我们把前两个表合并，$f \circ g = f(g(x))$ 就得到TBoxesTyiTables。

最后算法变成这样：

state <- plaintext
for r = 1 to 9:
	ShiftRows
	TBoxesTyiTables
	XORTables
ShiftRows
Tboxes
ciphertext <- state

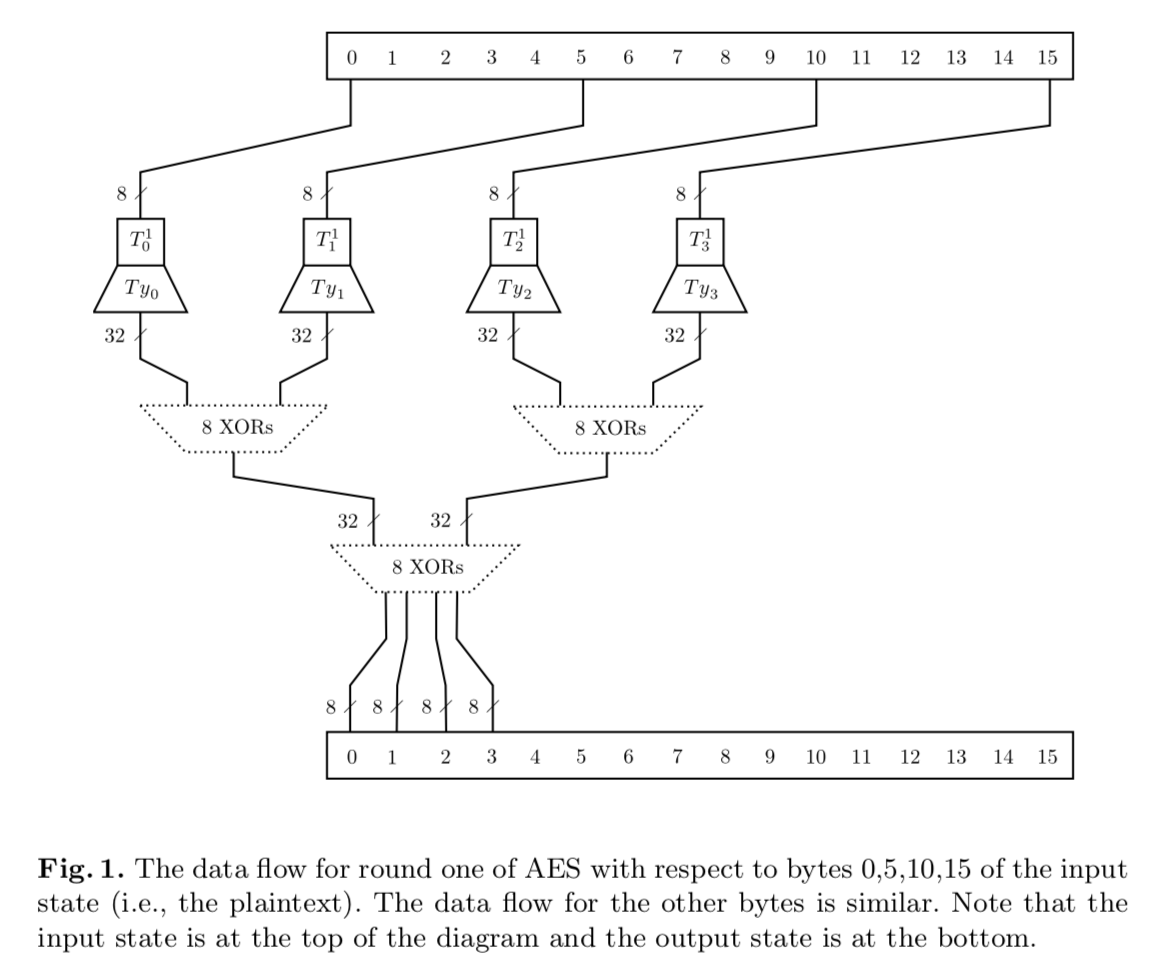
至此，所有的AES矩阵操作归结为查表操作。而查表操作是一对一的，在运行全过程可被监控的情况下，轮密钥很容易被推导。

疑惑

1. 内存中不直接暴露轮密钥吗（轮密钥不应该存在于内存中吗）？

   不，DRM的加解密操作中，内存中只有相关的表，以此实现加密解密。并非裸密钥（轮密钥）进行。如见OpenWhiteBox中，被序列化与被解析的是不同的表，在persistance.go中。key.txt其实是表的二进制表示。其中不包含任何的密钥的原始状态表示。密钥被混合在表中。

2. 为什么原生AES-128不安全？

   轮密钥只要有一轮泄漏，就可以推导出整个密钥。根据我们的设定，原生AES中每一轮都可以得到任何读写中间结果。假设$a$是第一轮密钥第一个字节，那么仅有256种枚举方式，可向数据入口插入错误 ，例如0x00000000，只要枚举，或者 $a = S^{-1}\circ T_{y_0}^{-1}\circ (T_{y_0} \circ T^1_0)(0)$，$S$已知，$T_{y_0}^{-1}$可求，这样就可得到这个字节。这样4x4都出来，原生密钥就都出现了。

保护性实现

针对AES的白盒安全保护，自02年来有很多实现。github.com/OpenWhiteBox/AES中有各种实现与密码分析。文[^ 1]描述了最初始的实现：chow‘s implementation。

chow的实现以输入输出编码(input and output encoding)、mixing bijections的方式来保护AES在WBAC下的安全。这也是许多变种设计过程中使用的思路。

• Encodings
• Mixing Bijections

Encodings

Encodings 意图给原生的表加上内/外的保护，使得在AES做矩阵变换的时候，并不直接地产生裸结果。这可以使得疑惑2条件不成立。这是用来保护TboxTyiTable的。假设原生的$T-Box/T_{y_i}$表为$T$, 现在以$f$为输入编码，$g$为输出编码，构建
$$
T’ = g \circ T \circ f^{-1}
$$
内编码不暴露的情况下，攻击者无法从一轮中的中间数据得到相应的映射。或者说，攻击者没有办法从这个$T’$中获得关于T的信息。考虑非线性$f$对4比特(one nibble)数据进行encoding，并采用concat的形式联合：
$$
f(x_0 || x_1) = f_1(x_0) || f_2(x_1),\ x_i\ is\ a\ nibble
$$
设这种encoding为$O$。$OT$没有泄漏任何关于$T$的信息。4比特可以产生$16!$种不重复的数值变换。对应地，每个字节就是$(16!)^2$种encoding。若加上output encoding, 则为$(16!)^2 (16!)^8$。这枚举是非常困难的。对于目标T表，以及任意非目标的$T’$表，都存在一个非线性映射$O’$, 使得$O’T’ = OT$。爆破理论上是不可行的。

另外，这种encoding是可以被networked的。不同的表可以被串联起来。这使得内部的推导会更难。
在Github.com/OpenWhiteBox/AES/的chow实现中：

// tyiEncoding encodes the output of a T-Box/Tyi Table / the input of a HighXORTable.
//
// All randomness is derived from the random source; round is the current round; position is the byte-wise position in
// the state matrix being stretched; subPosition is the nibble-wise position in the Word table's output.
func tyiEncoding(rs *random.Source, round, position, subPosition int) encoding.Nibble {
	label := make([]byte, 16)
	label[0], label[1], label[2], label[3] = 'T', byte(round), byte(position), byte(subPosition)

	return rs.Shuffle(label)
}

对T表的encoding就是4比特的。

在文[^ 1]的图里，是不包含了encoding部分的。在进行分析的时候我们有意抹去了encoding，因为encoding的安全性来自于外部。这不是算法安全性分析的范畴。

Mixing Bijections

Mixing Bijections是加密过程中增加的一个线性变换。用于对TboxTyiTable的扩散。encoding 实现了对密钥的混淆，每一轮中插入的Mixing Bijections则强化了密钥的扩散。被随机选择的Mixing Bijection变换都能够提高AES原生表的复杂性。作用在代码中耦合，会使得查表环节无法从TboxTyiTable的求解依赖于混入双射变换矩阵MB。根据chow的实现，选择一个GF(2)内的可逆矩阵MB，
于是我们是这样构造的。

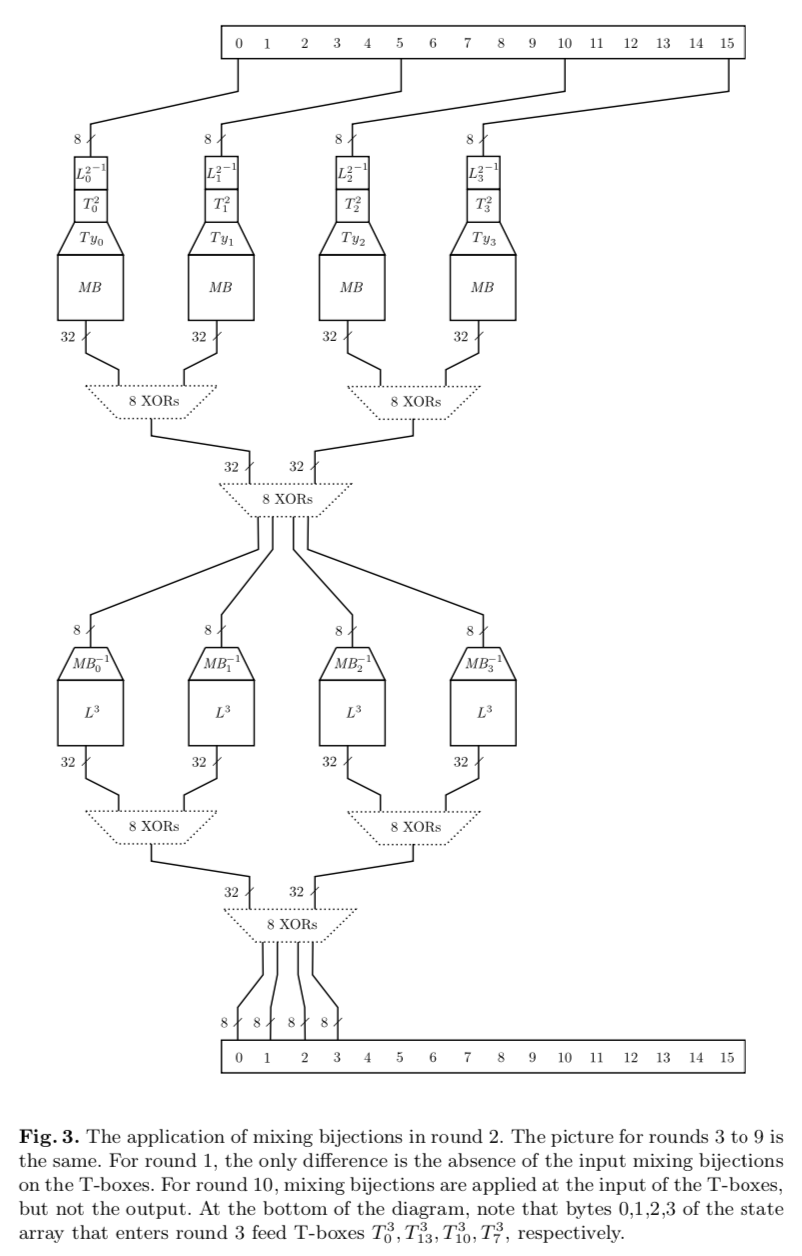
1. 由于第一轮，在输入的时候为明文/密文，这一轮应该用下文提及的外部编码（external encoding）来处理。这一轮的输入端不进行双射混合。
2. 第2到10轮，选择8比特到8比特的变换矩阵，附加在T表输入之前。
3. 1～9轮，在T表的输出端加上32-bit到32-bit的映射。

原来的TboxTyiTable表：
$$
T_{y_0}\circ T^2_0 \\
T_{y_1}\circ T^2_1 \\
T_{y_2}\circ T^2_2 \\
T_{y_3}\circ T^2_3 \\
$$

现在的$T’$表：
$$
MB \circ T_{y_0}\circ T^2_0 \circ {L^2_0}^{-1}\ (1) \\
MB \circ T_{y_1}\circ T^2_1 \circ {L^2_1}^{-1}\\
….
$$
$L$是8-bit到8-bit的输入mixing bijection, MB是32 -> 32的输出mixing bijection。这些表的最终结果被XOR起来。
为了下一轮计算可以进行，(1)中$MB$的效果需要被去除，而需要加上$L$。$MB^{-1}$作用于（1）产生的32bit结果，然后给每一个字节作用上$L^3$（此处为第三轮，所以为$L^3$），则结果可供给下一轮进行。
所以，Mixing Bijection的运行过程是，

1. 8bit$L{-1}$作用于输入$I$，得到$I_1$
2. TboxTyiTable作用于$I_1$，得到32bit值
3. 将4个32bit值XOR，得到中间值$I_2$
4. 32bit的$I_2$每个字节被$MB^{-1}$作用得到32bit中间值，然后被32->32$L$进行Mixing Bijection
5. 4个32bit值XOR成一个32bit，成为下一轮的state

外部编码

为了防止裸（raw）的明文到密文，或密文到明文的映射，以保护加密/解密器在特定环境下使用，可以给加密/解密器加上特定的外部编码。假定原来的解密器为$D_k$，则构建
$$
D’_k = G \circ D_k \circ F^{-1}
$$
$F$是输入编码，$G$是输出编码。这种方式在特定条件下可以保护DFA攻击[^ 4]。

[^1]: James A. Muir, A Tutorial on White-box AES
[^2]: S. Bhatkar, D. C. DuVarney, R. Sekar, Address obfuscation: an efficient approach to combat a broad range of memory error exploits, in Proceedings of the 12th USENIX Security Symposium. USENIX Association (2003)
[^3]: C. Linn, S.K. Debray. Obfuscation of executable code to improve resistance to static disassembly, in S. Jajodia, V. Atluri, and T. Jaeger, editors, Proceedings of the 10th ACM Conference on Computer and Communications Security, CCS 2003. ACM (2003), pp. 290–299
[^4]: White-Box Cryptography: Don’t Forget About Grey-Box Attacks
[^5]: WHITE-BOX CRYPTOGRAPHY AND AN AES IMPLEMENTATION
[^6]: 详见CANSv7
[^7]: Biryukov A, Bouillaguet C, Khovratovich D. Cryptographic schemes based on the ASASA structure: black-box, white-box, and public-key[C]. In: Advances in Cryptology—ASIACRYPT 2014. Springer Berlin Heidelberg, 2014: 63–84.
[^10]: https://gongzheng.github.io/